scihub 命令行工具

https://github.com/SuperBruceJia/Sci-Hub-Paper-Download-shell

目录结构

1
2
3
4
5
6
7
8
9
10
11
12
13
.
├── ISSUE_TEMPLATE
│   ├── bug_report.md
│   └── feature_request.md
├── LICENSE
├── __pycache__
│   └── scihub.cpython-39.pyc
├── README.md
├── sci-downloads.py
├── scihub.py
└── scihub.pyc

2 directories, 8 files

记得要把脚本 scihub.py sci-downloads.py 两个文件中的 python 地址写对。。。

EMCEE 的使用

如果你学习宇宙学,那么有时候就需要对模型进行参数限制, 本文以使用哈勃参量限制宇宙学
参数为例,展示如何使用emcee.其实还是蛮简单的.

贝叶斯

首先我们要有一丢丢贝叶斯统计的基础知识, 也就是贝叶斯公式:

$P(A|B)$ 后验概率, 也就是我们最终要得到的参数概率分布
$P(A)$ 先验概率,也就是我们认为的参数的概率分布, 最终结果还是要看$P(A|B)$
$P(B|A)$ 似然函数, 说白了就是模型,就是我们的理论函数,函数中有我们要求的参数
$P(B)$ 这个一般是取1…不是很明白这个是啥意思具体…

所以,我们只需要两样东西: 模型的函数形式和模型中参数的先验分布,而且先验分布一般设置为均匀分布…so easy!

Python emcee 模块

文档: https://emcee.readthedocs.io/en/stable/

下载啥的就不说了

上例子, 好吧其实例子文档里有…但是这个例子是自己跑的…

导入需要的模块…

1
2
3
4
import emcee
import numpy as np
from matplotlib import pyplot as plt

数据:

哈勃参量数据:

1
2
3
4
5
6
7
8
9
10
x=np.array([0.07,0.09,0.12,0.17,0.1791,0.1993,0.2,0.27,0.28,0.3519,0.3802,0.4,0.4004,0.4247,0.4497,0.4783,0.48,0.5929,0.6797,0.7812,0.8754,0.88,0.9,1.037,1.3,1.363,1.43,1.53,1.75,1.965])
y=np.array([69,69,68.6,83,75,75,72.9,77,88.8,83,83,95,77,87.1,92.8,80.9,97,104,92,105,125,90,117,154,168,160,177,140,202,186.5])
yerr=np.array([19.6,12,26.2,8,5,5,29.6,14,36.6,14,13.5,17,10.2,11.2,12.9,9,62,13,8,12,17,40,23,20,17,33.6,18,14,40,50.4])

error_range=[yerr*1,yerr*1]
plt.errorbar(x,y,yerr=error_range,fmt='o',ecolor='r',color='b',elinewidth=1,capsize=2,ms=2,mfc='y',mec='b')
plt.xlabel('z')
plt.ylabel('$H (z)[km s^-1 Mpc^-1]$')
plt.show()

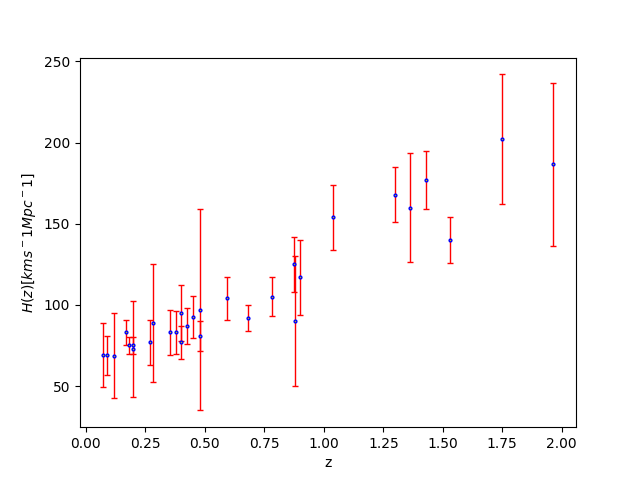
模型:

普普通通的LCDM模型:

$H(z)$是数据的理论模型,右边$H_0$, $\Omega_m$, $\omega$是我们要求的参数, $z$是自变量,红移.

先验函数定义

一般来说,我们采用均匀分布, 根据以前的观测,我们大致知道哈勃常数$H_0$大概在60-70,
物质密度大概是0.3,暗能量参数$\omega$大概是-1,据此设定这些均匀分布的取值范围,不用很精确.
emcee需要的是先验函数的ln形式,所以聪明的你应该看懂了下面的代码.

1
2
3
4
5
6
def log_prior(theta):
    H_0, m, w = theta
    if 20.0 < H_0 < 80.0 and 0.0 < m < 1.0 and -2 < w < 2:
        return 0.0
    return -np.inf

似然函数的定义

似然函数(一般使用这个形式):

其中

当然,需要$\mathcal{L}$的ln形式,代码如下

1
2
3
4
5
6
def log_likelihood(theta,x,y,yerr):
  H_0,m,w = theta
  model=H_0*np.sqrt(m*(1+x)**3+(1-m)*(1+x)**(3*(1+w)))
  sigma2=yerr**2
  return -0.5*np.sum((y-model)**2/sigma2)

ok,最后我们的概率函数就是把先验函数和似然函数相乘就行了.写代码要注意取ln

1
2
3
4
5
6
def log_probability(theta, x, y, yerr):
    lp = log_prior(theta)
    if not np.isfinite(lp):
        return -np.inf
    return lp + log_likelihood(theta, x, y, yerr)

emcee 采样

1
2
3
4
5
6
7
8
9
pos = np.array([67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.,67.,0.3,-1.]).reshape(32,3) + 1e-4 * np.random.randn(32, 3)
nwalkers, ndim = pos.shape
sampler = emcee.EnsembleSampler(nwalkers, ndim, log_probability, args=(x, y, yerr))


state = sampler.run_mcmc(pos, 1000)
sampler.reset()
sampler.run_mcmc(state, 100000, progress=True);

想要跑mcmc,我么需要一个初始状态矩阵pos,这个矩阵具有维度(nwalkers,ndim),ndim是参数的个数, nwalkers
不是很懂是什么意思,应该是马尔科夫链那个矩阵的一个维度, 这里把它设置为32,你也可以看看设置为其他值会有什么影响.在这个例子中,nwalkers=32,ndim=3,也就是3个参数值一组,一共32组,pos里参数值根据经验来定,这样应该收敛比较快,这里取值为$H_0=67$, $\Omega_m=0.3$, $\omega=-1$ 注意还要 加一个相同形状的小随机数矩阵,否者
会报错:”Initial state has a large condition number. Make sure that your walkers are linearly
independent for the best performance”.条件数是啥我也不是很清楚…emcee.EnsembleSampler 里,log_probability是我们之前定义的参数概率函数,args里是
所有非参数变量.最后我们得到了一个emcee对象,sampler.

之后我们先跑了1000次,并把这时的状态矩阵存到state里,重新设置一下采样器,用这个新的状态矩阵来作为我们采样
的起始位置,跑个100000次先.参数progress=True会显示当前还有多长时间算完.我的破电脑跑这个10w次需要5min左右.

结果可视化

可以用以下代码把采样过程展现出来

1
2
3
4
5
6
7
8
9
10
11
12
13
fig, axes = plt.subplots(3, figsize=(10, 7), sharex=True)
samples = sampler.get_chain()
labels = ["$H_0$", "$\Omega_m$", "$\omega$"]
for i in range(ndim):
    ax = axes[i]
    ax.plot(samples[:, :, i], "k", alpha=0.3)
    ax.set_xlim(0, len(samples))
    ax.set_ylabel(labels[i])
    ax.yaxis.set_label_coords(-0.1, 0.5)

axes[-1].set_xlabel("step number");
plt.show()

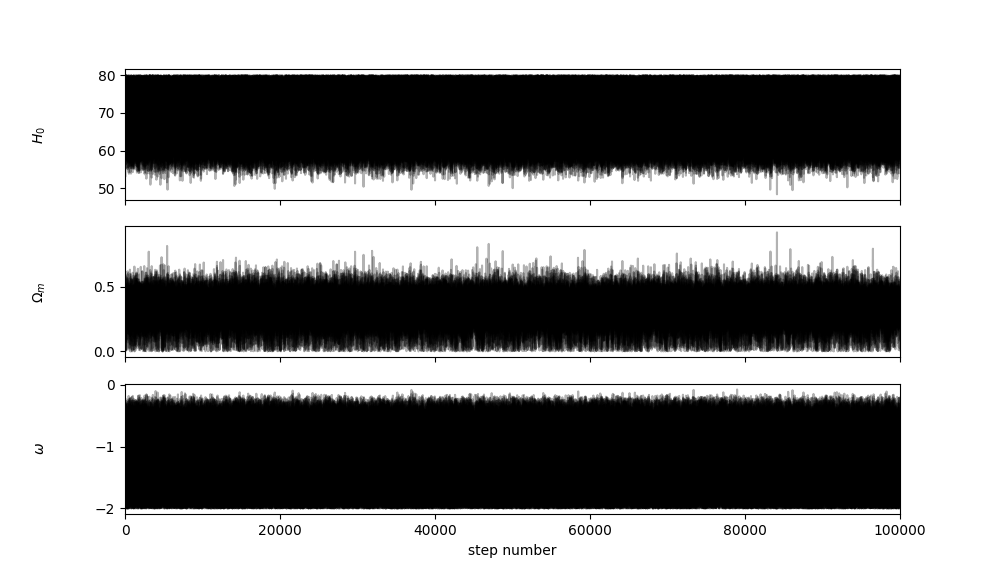
如果你看到类似上面这种图,说明mcmc收敛了.
之后我们用get_chain得到采样链并展平,用Python的Corner模块画参数的后验概率图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
flat_samples = sampler.get_chain(discard=100, thin=15, flat=True)
print(flat_samples.shape)

import corner

fig = corner.corner(
    flat_samples,truths=[67, 0.3,-1],labels=["$H_0$","$\Omega_m$","$\omega$"],
                    show_titles=True, title_kwargs={"fontsize": 12},
                    bins = 20
);

plt.show()

fig.savefig('/home/qinjin/hubble.pdf',dpi=600,format='pdf')

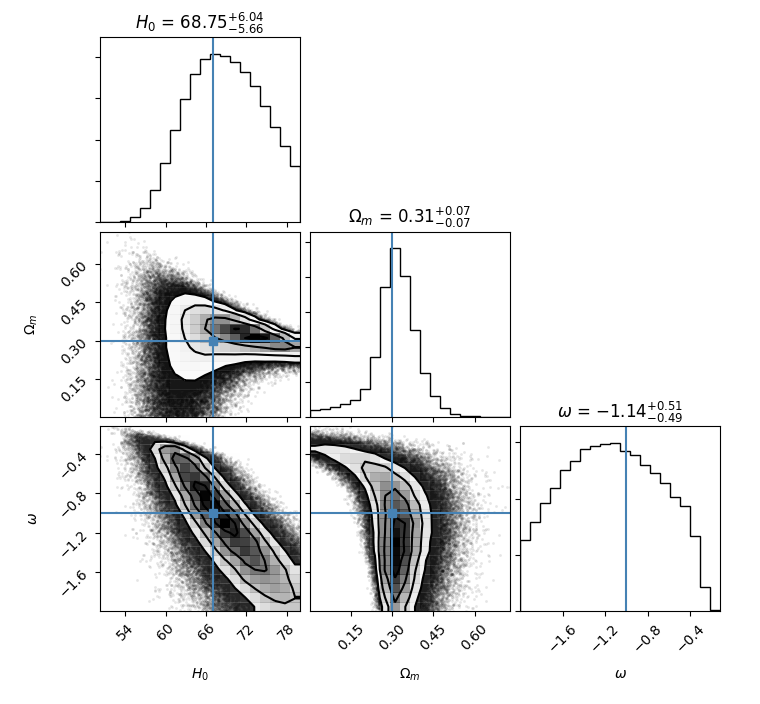
注意不要用eps,导出的图非常难看,可以先导出为pdf或者png再转换成eps.

其中trues是我们之前状态矩阵参数的初始值,也就是图中的直线.这样我们就把模型

里的3个参数用mcmc的方法限制出来了.结果展示:

1
2
3
4
5
6
7
8
9
from IPython.display import display, Math

for i in range(ndim):
    mcmc = np.percentile(flat_samples[:, i], [16, 50, 84])
    q = np.diff(mcmc)
    txt = "\mathrm{{{3}}} = {0:.3f}_{{-{1:.3f}}}^{{{2:.3f}}}"
    txt = txt.format(mcmc[1], q[0], q[1], ["$H_0$","$\Omega_m$","$\omega$"][i])
    display(Math(txt))

不知道为什么多了两个$符号…

FLRW度规下的宇宙学距离

均匀各项同性下的宇宙时空符合$FLRW $度规

Coordinate distance 坐标距离

$(1)$ 式 中的 $r $为 coordinate distance
这是可以从度规中遇到的第一个距离的概念, 它表示径向的坐标读数.

Proper distance 本征距离

Proper distance 代表某一特定时刻, 两物体间的距离, 因为定死了时间, 所以不考虑宇宙的膨胀, 但是在不同时刻, Proper distance 因宇宙膨胀而不同的, Proper distance 是时间的函数.

观察者与光源位于同一视线, 且位于相同的时刻, 于是 $d\theta$, $d\phi$, $dt$ 为 $0$

可以看出 Proper distance $s(t)$ 依赖于时间. 这个距离可以看做两物体间的物理距离, 但是不可以直接观测.

Comoving distance 共动距离

顾名思义, 共动距离就是共动坐标系中两物体的空间距离., 需要考虑到宇宙的膨胀, 并且由光从物体到观测点走过的距离定义. 一般来说, 观测点为坐标原点, 观察者与物体位于同一视线, $d\theta$, $d\phi$ 为 $0$, 于是我们有

其中, $+$表示发射的光线, $-$ 表示接受的光线

观测当然是接受来自天体的光线, 等式右边取负号, 两边积分

光线在 $t_e$ 时刻从光源发出, 在$t_0$ 时刻被我们接受, 考虑宇宙的膨胀, 对尺度因子的倒数求积分. 因此, 共动距离与坐标距离的关系为

或者

可见, 共动距离在曲率$\kappa$ 为 $0$ 时, 与坐标距离 $r$ 等价. 与本征距离相同, 共动距离也是不可直接观测的.

Angular diameter distance 角直径距离

$(1)$ 式中可以看出, 计算角向的距离, 需要使用 coordinate distance 而不是 comoving distance

其中 $D$ 为 某一天体的 proper distance 大小, 于是便可以定义

根据共动距离与坐标距离的关系, 可以得到

Luminosity 光度距离

这个逻辑上类似于角直径距离, 先不写

问题 如何将 曲率为 -1 的极坐标系的转化为笛卡尔坐标系?

比如 笛卡尔坐标系下